Diện tích hình thoi
Hình thoi là một tứ giác có bốn cạnh bằng nhau, chúng tạo thành một hình bình hành với hai cặp cạnh liền kề có độ dài giống nhau và hai đường chéo thì vuông góc với nhau. Trước khi tìm hiểu diện tích của hình thoi, cùng điểm qua tính chất của hình thoi:
Các góc đối diện bằng nhau.
Các cạnh của hình thoi bằng nhau.
Hai đường chéo vuông góc với nhau và cắt tại giao điểm của chúng hay chính là trung điểm của mỗi đường.
Hai đường chéo chính là các đường phân giác của mỗi góc trong hình thoi.
Hình thoi sở hữu tất cả các đặc điểm của hình bình hành: cặp cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm mỗi đường.
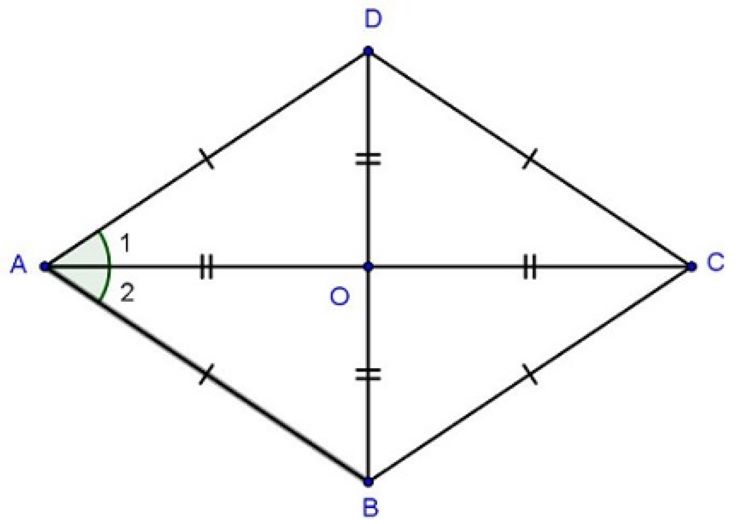
Tính chất của hình thoiDấu hiệu 1: Tứ giác có 4 cạnh bằng nhau là hình thoi
Dấu hiệu 2: Tứ giác có hai đường chéo vuông góc với nhau, cắt nhau tại trung điểm của mỗi đường hình thoi là hình thoi.
Dấu hiệu 3: Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Dấu hiệu 4: Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Dấu hiệu 5: Hình bình hành có đường chéo là đường phân giác của một góc là hình thoi.
>> Tham khảo: Các nước đông nam á
Diện tích của hình thoi được tính bằng một nửa tích độ dài của hai đường chéo. Đường chéo của hình thoi là đường thẳng nối 2 đỉnh đối diện với nhau. Hai đường chéo này sẽ cắt nhau tại một điểm và vuông góc với nhau. Công thức tính như sau:
S = 1/2 x (d1 x d2)
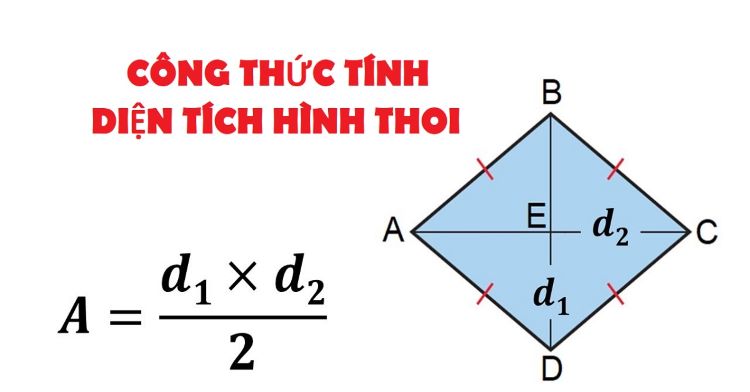
Công thức tính diện tích của hình thoi
Trong đó:
S là diện tích của hình thoi
d1 và d2 lần lượt là độ dài của hai đường chéo của hình thoi.
Ví dụ: Cho hình thoi có độ dài 2 đường chéo lần lượt là 6cm, 8cm. Tính diện tích của hình thoi trên.
Áp dụng công thức ta có: S = ½ x (6 x 8)= 24
Để tính chu vi của hình thoi, ta lấy tổng độ dài của tất cả các cạnh hoặc nhân độ dài của một cạnh với 4. Do đó, công thức tính chu vi được thể hiện như sau:
P = a + a + a + a = 4a
Trong đó:
P: Chu vi của hình thoi
a: Độ dài của một cạnh trong hình thoi (các cạnh hình thoi có độ dài bằng nhau)
Ví dụ: Cho một hình thoi có độ dài cạnh là 6cm. Tính chu vi hình thoi trên?
P = 6 x 4 = 24cm
Dưới đây là 3 dạng bài tập cơ bản liên quan đến diện tích hình thoi:
Dạng 1: Cho độ dài hai đường chéo, tính diện tích
Phương pháp giải: Khi biết độ dài 2 đường chéo, áp dụng tính diện tích của hình thoi theo công thức.
Đề bài: Cho hình thoi có độ dài hai đường chéo lần lượt là d1 = 8 và d2 = 12. Tính diện tích của hình thoi.
Cách giải:
Áp dụng công thức: S = ½ x d1 x d2
Thay vào độ dài của hai đường chéo ta có: S = ½ x 8 x 12= 48 cm2
Dạng 2: Cho chiều cao và cạnh đáy của hình thoi
Phương pháp giải: Để tính diện tích của hình thoi trong bài tập này chúng ta áp dụng công thức tính diện tích dựa vào chiều cao và cạnh đáy của nó. Công thức áp dụng S = h x a
Trong đó:
S: Diện tích của hình thoi
h: Độ dài chiều cao của hình thoi
a: Độ dài cạnh đáy của hình thoi
Ví dụ:Cho một hình thoi có độ dài cạnh AB = CD = BC = DA = 6cm và chiều cao của hình thoi là 4cm. Tính diện tích của hình thôi đã cho.
Lời giải: S = h x a = 4 x 6 = 24 cm2
Dạng 3: Cho thông tin về các góc và cạnh của hình thoi
Ví dụ: Cho một hình thoi có độ dài cạnh bằng 6cm và một góc trong của hình thoi là 60 độ. Từ đó, tính diện tích của hình thoi.
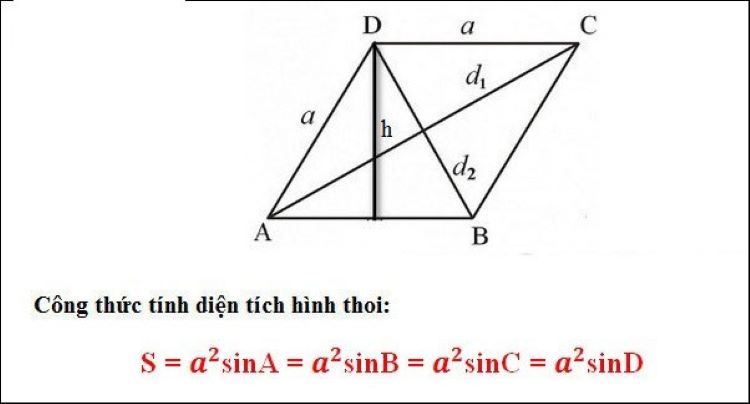
Công thức tính diện tích của hình thoi khi biết cạnh và một góc của hình thoi
Lời giải:
Áp dụng công thức diện tích tam giác: S = ½ x a x b x sin(C).
Trong đó, a và b là hai cạnh của tam giác, C nằm là góc giữa hai cạnh
Vì hình thoi có cặp góc đối nhau bằng nhau, nên góc giữa hai cạnh này là 60 độ.
Đặt a = b = 6 (do độ dài cạnh của hình thoi bằng nhau)
Diện tích tam giác: S1 = ½ x 6 x 6 x sin(60) = 9√3
Diện tích của hình thoi là S2 = 2x S1= 18√3
Tạm kết
Trên đây là những thông tin xoay quanh về diện tích hình thoi. Hy vọng qua bài viết bạn đã có câu trả lời phù hợp nhất về thắc mắc về cách tính diện tích, chu vi hình thoi.