Diện tích hình thoi
Hình thoi là một tứ giác đặc biệt trong hình học phẳng, được định nghĩa là tứ giác có bốn cạnh bằng nhau. Đây cũng là một trường hợp riêng của hình bình hành, với nhiều tính chất đối xứng nổi bật.
Hình thoi có những đặc điểm cơ bản sau:
Bốn cạnh bằng nhau
Khác với hình chữ nhật (có hai cặp cạnh đối bằng nhau), hình thoi có cả bốn cạnh có cùng độ dài.
Hai đường chéo vuông góc
Đặc điểm quan trọng nhất của hình thoi là hai đường chéo không chỉ cắt nhau tại trung điểm của mỗi đường mà còn vuông góc với nhau.
Hai đường chéo là trục đối xứng
Hai đường chéo của hình thoi đồng thời là hai đường phân giác của các góc trong hình, chia hình thoi thành bốn tam giác vuông bằng nhau.
Góc đối bằng nhau
Trong hình thoi, hai cặp góc đối luôn bằng nhau, kế thừa tính chất của hình bình hành.
Hình thoi vừa có tâm đối xứng vừa có trục đối xứng
Tâm đối xứng chính là giao điểm của hai đường chéo, còn hai đường chéo lại là hai trục đối xứng của hình.
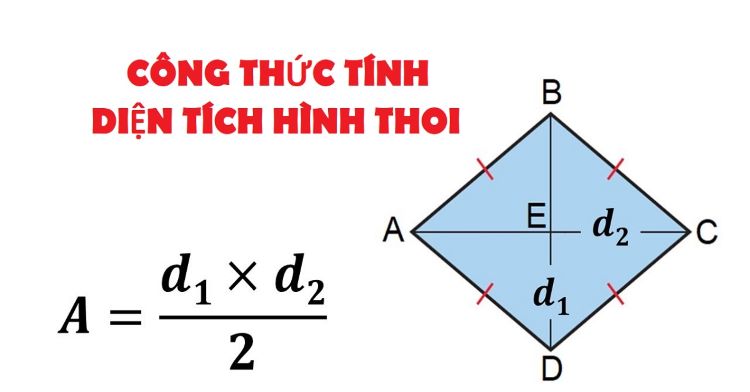
Công thức tính diện tích của hình thoiDiện tích của hình thoi có thể tính dễ dàng nhờ vào đặc điểm hai đường chéo vuông góc và cắt nhau tại trung điểm. Công thức cơ bản nhất được dùng là:
S=(d₁ × d₂) / 2
Trong đó:
S là diện tích
d₁ và d₂ là độ dài hai đường chéo.
Ví dụ: Nếu hình thoi có hai đường chéo lần lượt dài 6 cm và 8 cm, diện tích sẽ tính như sau:
S=(6 × 8) / 2=24 cm² .
Ngoài ra, nếu biết cạnh a và chiều cao h (chiều cao ứng với một cạnh của hình thoi), diện tích còn có thể tính bằng công thức:
S=a × h
Nhưng công thức phổ biến và thường được áp dụng nhất vẫn là:
S=(d₁ × d₂) / 2
bởi vì hai đường chéo thường dễ xác định hơn và phản ánh trực tiếp đặc điểm hình học đặc biệt của hình thoi.
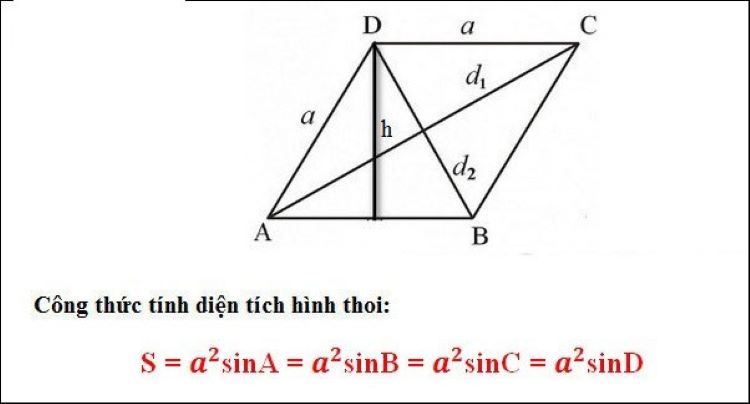
Công thức tính diện tích của hình thoi khi biết cạnh và một góc của hình thoiCông thức tính diện tích khá ngắn gọn:
S=(d₁ × d₂) / 2
Trong đó, d₁ và d₂ là độ dài hai đường chéo của hình thoi. Để nhớ công thức này lâu hơn và tránh nhầm lẫn, bạn có thể áp dụng một vài mẹo học nhanh dưới đây.
Nhớ câu “ tích hai chéo, chia đôi”
Hãy học thuộc thành câu ngắn gọn: diện tích =tích hai đường chéo rồi chia đôi. Cách này giúp tránh bị quên phép chia 2, vốn là phần dễ bị bỏ sót nhất.
Liên tưởng trực quan
Hãy tưởng tượng hai đường chéo chia hình thoi thành bốn tam giác vuông nhỏ bằng nhau. Tổng diện tích của bốn tam giác này chính là diện tích , nên lấy tích hai đường chéo chia đôi là đủ.
Ghi chú trực tiếp trên hình vẽ
Khi học hoặc giải bài tập, vẽ một hình thoi, kẻ hai đường chéo và ghi ngay công thức lên hình. Việc kết hợp chữ và hình ảnh giúp não bộ ghi nhớ tốt hơn.
Ôn lại bằng ví dụ số cụ thể
Ví dụ, nếu d₁=10 cm và d₂=8 cm, tính diện tích như sau:
S=(10 × 8) / 2=40 cm² .
Làm vài phép tính như vậy, bạn sẽ nhớ công thức tự nhiên hơn.
Chỉ cần nhớ: diện tích hình thoi=tích hai đường chéo chia đôi và kết hợp hình vẽ minh họa, bạn sẽ dễ dàng ghi nhớ công thức này lâu dài và chính xác khi làm bài.

Ứng dụng trong xây dựngDiện tích được tính khá đơn giản bằng công thức S=(d₁ × d₂) / 2, trong đó d₁ và d₂ là độ dài hai đường chéo. Tuy nhiên, để tránh sai sót, bạn nên chú ý một số điểm sau.
Xác định đúng hai đường chéo
Đường chéo của hình thoi là đoạn thẳng nối hai đỉnh không kề nhau và cắt nhau tại trung điểm. Đôi khi, nếu vẽ hình không chuẩn, dễ nhầm đường chéo với cạnh hoặc đường nối không vuông góc.
Đo chính xác độ dài đường chéo
Khi tính diện tích dựa trên đường chéo, việc đo thiếu hoặc dư vài mm cũng có thể làm kết quả sai lệch đáng kể, nhất là với hình thoi có kích thước lớn.
Nhớ chia đôi sau khi nhân
Một lỗi hay gặp là quên chia 2 sau khi nhân hai đường chéo. Để tránh điều này, nên học thuộc câu: diện tích bằng tích hai đường chéo chia đôi.
Chỉ áp dụng khi biết chính xác hai đường chéo
Nếu chỉ biết độ dài cạnh và một góc, cần dùng công thức khác:
S=a² × sinA
Trong đó a là cạnh và A là góc bất kỳ của hình thoi.
Kiểm tra đơn vị đo lường
Hãy đảm bảo hai đường chéo cùng một đơn vị đo (cm, m, mm… ). Sau khi tính toán, đừng quên ghi kèm đơn vị diện tích như cm² hoặc m² .