Diện tích hình thoi
Khi học toán hình học, một trong những dạng hình cơ bản mà bạn thường gặp là hình thoi. Đây là một tứ giác đặc biệt, có bốn cạnh bằng nhau và các cặp góc đối bằng nhau. Hình thoi có thể được xem như một trường hợp riêng của hình bình hành, nhưng mang tính đối xứng cao hơn.
Việc tính diện tích của hình thoi không chỉ quan trọng trong toán học mà còn có nhiều ứng dụng thực tế. Chẳng hạn, khi bạn cần đo diện tích một miếng vải, một ô ruộng hay một thiết kế kiến trúc có dạng hình thoi, công thức tính diện tích sẽ giúp bạn tính toán nhanh chóng và chính xác.
Ngoài ra, trong các kỳ thi toán học, diện tích của hình thoi là dạng bài thường xuyên xuất hiện. Việc nắm chắc công thức và cách áp dụng sẽ giúp bạn giải quyết nhiều dạng bài tập từ cơ bản đến nâng cao.
Đặc điểm nhận biết hình thoi
Hình thoi có các đặc điểm sau:
Bốn cạnh bằng nhau.
Hai đường chéo vuông góc với nhau.
Các đường chéo cắt nhau tại trung điểm.
Góc đối bằng nhau, tổng hai góc kề nhau bằng 180°.
Những đặc điểm này chính là cơ sở để suy ra công thức tính diện tích.
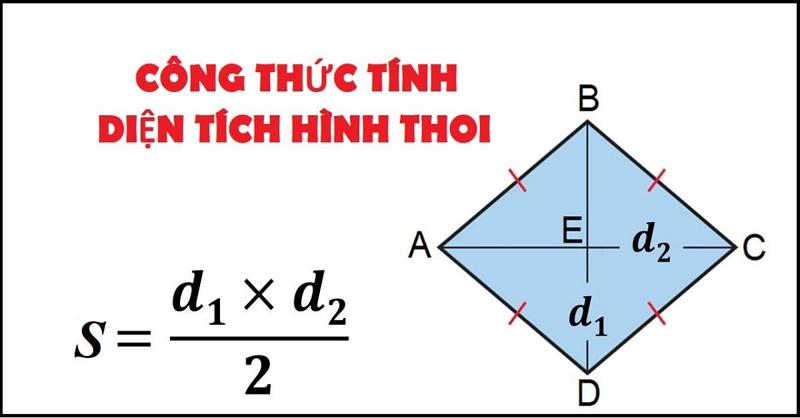 Công thức tính diện tích của hình thoi bằng hai đường chéo
Công thức tính diện tích của hình thoi bằng hai đường chéoCó nhiều cách khác nhau để tính diện tích hình thoi, tùy thuộc vào dữ kiện đề bài cho. Tuy nhiên, công thức thường gặp và dễ áp dụng nhất chính là dựa vào hai đường chéo.
Công thức tính diện tích của hình thoi:
S = (d1 × d2) / 2
Trong đó:
S là diện tích của hình thoi.
d1 và d2 là độ dài hai đường chéo của hình thoi.
Ví dụ: Nếu một hình thoi có hai đường chéo lần lượt là 8 cm và 10 cm, diện tích sẽ là:
S = (8 × 10) / 2 = 40 cm²
Ngoài ra, bạn có thể áp dụng một số công thức khác tùy trường hợp:
Nếu biết cạnh a và góc α giữa hai cạnh kề nhau:
S = a² × sin(α)
Nếu biết cạnh a và chiều cao h kẻ từ một đỉnh xuống cạnh đối diện:
S = a × h
Khi nào áp dụng từng công thức?
Nếu đề bài cho sẵn độ dài hai đường chéo → dùng công thức S = (d1 × d2) / 2.
Nếu cho cạnh và góc → dùng công thức S = a² × sin(α).
Nếu cho cạnh và chiều cao → dùng công thức S = a × h.
Như vậy, bạn chỉ cần linh hoạt lựa chọn công thức phù hợp để giải quyết nhanh gọn bài toán.
 Ví dụ bài toán tính diện tích của hình thoi
Ví dụ bài toán tính diện tích của hình thoiĐể hiểu rõ hơn, chúng ta cùng xem qua một số ví dụ cụ thể.
Ví dụ 1: Hình thoi có hai đường chéo d1 = 12 cm, d2 = 16 cm. Hãy tính diện tích của hình thoi.
Giải:
S = (12 × 16) / 2 = 96 cm²
Ví dụ 2: Hình thoi có cạnh a = 10 cm, góc kề α = 60°. Hãy tính diện tích.
Giải:
S = a² × sin(α)
S = 100 × sin(60°)
S ≈ 100 × 0.866 = 86.6 cm²
Ví dụ 3: Một hình thoi có cạnh a = 15 cm, chiều cao h = 12 cm. Hãy tính diện tích.
Giải:
S = a × h = 15 × 12 = 180 cm²
Nhận xét qua các ví dụ
Qua ba ví dụ trên, bạn có thể thấy rằng công thức tính diện tích của hình thoi khá linh hoạt. Tùy dữ kiện mà có thể chọn công thức phù hợp, tránh việc phải tính thêm nhiều bước trung gian. Điều này giúp tiết kiệm thời gian khi làm bài.
 Ứng dụng thực tế của hình thoi trong kiến trúc
Ứng dụng thực tế của hình thoi trong kiến trúcKhông chỉ dừng lại ở bài tập toán, công thức tính diện tích của hình thoi còn được ứng dụng nhiều trong đời sống.
Trong kiến trúc và xây dựng, người ta sử dụng công thức này để tính diện tích các mảng tường, mái nhà hoặc cửa sổ có dạng hình thoi. Điều này giúp dự trù vật liệu chính xác, tránh lãng phí.
Trong nông nghiệp, diện tích của hình thoi thường được dùng để đo các thửa ruộng, ao hồ hoặc khu đất có hình dạng đặc biệt. Nhờ đó, nông dân có thể tính toán được năng suất dự kiến hoặc lượng phân bón cần thiết.
Trong thiết kế thời trang và trang trí, họa tiết hình thoi xuất hiện rất phổ biến. Việc nắm được công thức tính diện tích giúp nhà thiết kế cân đối tỷ lệ và bố cục hợp lý.
Ứng dụng trong toán học và khoa học
Trong toán học, diện tích của hình thoi là cơ sở để phát triển nhiều bài toán nâng cao, như chứng minh hình học, bài toán tọa độ hay các bài liên quan đến vector. Trong vật lý, công thức diện tích còn được áp dụng trong các phép tính liên quan đến hình dạng vật thể.
Để học thuộc công thức tính diện tích của hình thoi, bạn có thể áp dụng một số mẹo sau:
Gắn công thức với hình ảnh: tưởng tượng hai đường chéo cắt nhau, nhân hai số đó rồi chia đôi.
So sánh với diện tích tam giác: vì hai tam giác tạo thành từ hai đường chéo chính là cơ sở của công thức.
Dùng thơ hoặc câu ngắn gọn: "Nhân hai chéo, chia đôi ngay, diện tích hiện bày liền trong tay".
Việc biến công thức thành một câu vần điệu sẽ giúp bạn dễ nhớ và ít nhầm lẫn.
Lỗi thường gặp khi tính diện tích của hình thoi
Quên chia đôi khi áp dụng công thức (d1 × d2) / 2.
Nhầm lẫn giữa cạnh và đường chéo.
Dùng sai đơn vị đo, chẳng hạn lấy cm và m cùng tính trong một công thức.
Chú ý tránh những lỗi này để kết quả luôn chính xác.
Diện tích hình thoi là một chủ đề cơ bản nhưng vô cùng quan trọng trong toán học và đời sống. Bằng cách nắm vững công thức và biết cách áp dụng linh hoạt trong từng trường hợp, bạn sẽ dễ dàng giải quyết nhiều dạng bài tập khác nhau. Đồng thời, hiểu rõ ý nghĩa thực tế sẽ giúp bạn thấy rằng toán học không hề khô khan mà gắn bó mật thiết với cuộc sống.>> Tham khảo: Vải bạt chống cháy