|
[MỤC LỤC]
1. Hình thoi là hình gì?
2. Tính chất và dấu hiệu nhận biết một hình thoi
3. Công thức tính diện tích hình thoi
4. Chu vi của hình thoi
5. Những lưu ý khi làm bài tính toán diện tích
6. Các dạng bài tập liên quan đến tính diện tích hình thoi
|
Diện tích hình thoi
Hình thoi là một tứ giác sở hữu bốn cạnh bằng nhau. Cùng có thể coi hình thoi là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.
Khi một hình thoi nếu sở hữu bốn góc vuông trong bằng nhau thì hình thoi đó được xác định là hình vuông. Như vậy, hình vuông là một trường hợp đặc biệt của hình thoi bởi hình vuông có bốn cạnh dài bằng nhau và có bốn góc vuông.
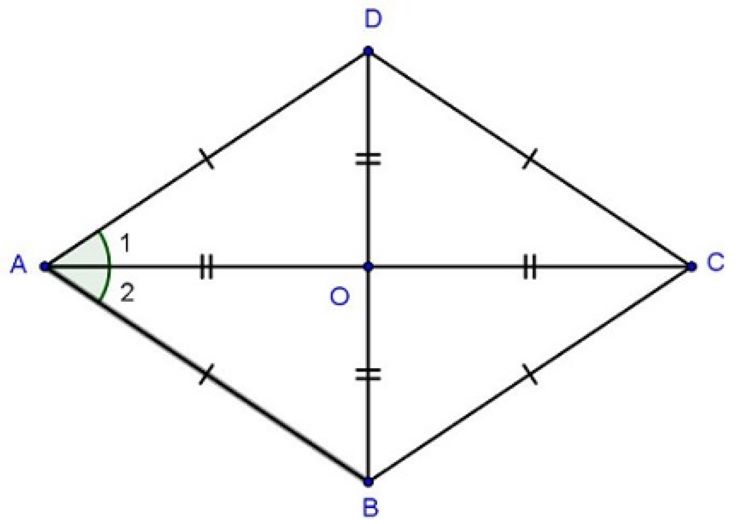
Đặc điểm của hình thoi
Kết luận:
Mọi hình vuông đều là hình thoi, tuy nhiên không phải hình thoi nào cũng là hình vuông.
Mọi hình thoi đều là hình bình hành, tuy nhiên không phải hình bình hành nào cũng là hình thoi.
Tính chất:
Hình thoi là hình học đặc biệt có những tích chất sau đây:
Các góc đối nhau thì bằng nhau.
Các cạnh hình thoi đều bằng nhau.
Hai đường chéo của hình thoi sẽ vuông góc với nhau và chúng cắt nhau tại trung điểm của mỗi đường chéo.
Hai đường chéo của hình thoi là các đường phân giác của các góc của hình thoi.
Hình thoi sở hữu tất cả tính chất của một hình bình hành
Dấu hiệu nhận biết:
Để nhận biết một hình học có phải là hình thoi hay không, ta cần dựa những dấu hiệu cơ bản dưới đây:
Dấu hiệu 1: Hình tứ giác sở hữu 4 cạnh bằng nhau là hình thoi.
Dấu hiệu 2: Tứ giác có 2 đường chéo chính là đường trung trực của nhau thì là hình thoi.
Dấu hiệu 3: Tứ giác có 2 đường chéo cũng là đường phân giác của cả bốn góc thì là hình thoi.
Dấu hiệu 4: Hình bình hành sở hữu hai cạnh kề bằng nhau là hình thoi.
Dấu hiệu 5: Hình bình hành sở hữu hai đường chéo vuông góc với nhau là hình thoi.
Dấu hiệu 6: Hình bình hành có một đường chéo là đường phân giác của một góc cũng là hình thoi.
>> Tham khảo: Các nước đông nam á
Công thức tính diện tích của hình thoi được phát biểu như sau: Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo của hình thoi.

Công thức tính diện tích của hình thoi
Công thức: S = ½ (d1 x d2) = a x h
Trong đó:
- S là diện tích của hình thoi
- d1, d2 là độ dài hai đường chéo của hình thoi
- h là chiều cao của hình thoi
- a là cạnh của hình thoi
Bên cạnh đó, ta cũng có thể tính diện tích của hình thoi dựa vào hệ thức trong tam giác (nếu đã có được số đo góc của hình thoi):
S = a² . sin A = a² . sin B = a² . sin C = a² . sin D
Trong đó:
- S: Diện tích của hình thoi
- a: Kích thước độ dài của cạnh bên
- α: Số đo một góc trong bất kỳ thuộc hình thoi.
Ví dụ: Cho hình thoi ABCD có độ dài 2 đường chéo là AC= 8cm, BD= 6 cm. Tính diện tích hình thoi ABCD?
Giải
Diện tích hình thoi ABCD là S= ½ x AC x BD= ½ x 8 x 6= 24
Tham khảo: Bây giờ là mấy giờ ở Mỹ?
Muốn tính được chu vi của hình thoi, ta chỉ cần tổng tất cả độ dài của tất cả các cạnh hay chính bằng kích thước của 1 cạnh đem nhân 4. Như vậy ta được công thức tính toán chu vi như sau:
P = a + a + a + a = 4a
Trong đó:
P: Chu vi của hình thoi
a: Độ dài của một cạnh trong hình thoi

Cách tính chu vi hình thoi
Ví dụ: Cho 1 hình thoi có tên là ABCD với độ dài cạnh là 4cm. Vậy chu vi hình thoi này bao nhiêu?
Giải
Ta có a = 4 cm
Suy ra chu vi của hình thoi này là: C= 4 x 4 = 16 (cm)
Tham khảo: dịch vụ seo website chuyên nghiệp
Trong các bài tập, hoặc bài kiểm tra thường có nhiều dạng bài tính diện tích. Do đó khi làm bài bạn cần đọc kỹ đề và lưu ý những điểm sau đây:
Khi đề bài cho độ dài các cạnh có đơn vị khác nhau, thì trước hết cần quy đổi về cùng một đơn vị đo độ dài.
Đối với bài toán so sánh diện tích các hình, cũng cần lưu ý đổi về cùng đơn vị đo diện tích của các hình. Nếu chúng khác nhau, bạn cần quy đổi về cùng một đơn vị đo rồi mới tiến hành so sánh.
Thực hiện kiểm tra lại kết quả ít nhất 2.
Dạng 1: Tính diện tích của hình thoi dựa vào đường chéo
Với dạng bài này bạn cần tính toán để xác định được độ dài 2 đường chéo dựa vào dữ kiện bài cho. Sau đó áp dụng công thức và tính.
Ví dụ 1: Tính diện tích của hình thoi cho biết độ dài cạnh bằng 15cm và một trong 2 đường chéo của hình trên bằng 18 cm.
Giải
Gọi độ dài đường chéo d1 là 18cm, độ dài cạnh hình thoi là 15cm và đường chéo d2.
Dựa vào tính chất của hình thoi, ta có hai đường chéo vuông góc với nhau, cắt nhau tại chung điểm của mỗi đường. Do vậy tạo nên bốn tam giác vuông.
Áp dụng định lý Py-ta-go ta tính được độ dài đường chéo d2:
d2 = 2 x √(15² – 9²) = 2 x 12 = 24
Vậy Diện tích của hình thoi trên là S1 = ½ ( 18 x 24) = 216 cm²
Dạng 2: Tính diện tích của hình thoi dựa vào chiều cao và cạnh đáy
Do hình thoi có hai cạnh bên và đáy bằng nhau. Do đó, chúng ta có áp dụng công thức sau để tính diện tích của hình thoi:
S = a x h
S là diện tích
a là độ dài cạnh đáy
h là chiều cao của hình thoi
Ví dụ 2: Tính diện tích của hình thoi có biết chiều cao 6cm và độ dài cạnh đáy là 100mm.
Giải
Đổi: 100mm = 10cm.
Vậy Độ dài cạnh đáy của hình thoi là 10cm.
Gọi S là diện tích của hình thoi, ta có: S = a x h = 10 x 6 = 60cm².
Dạng 3: Tính diện tích dựa theo công thức lượng giác
Hình thoi có độ dài cạnh đáy là a, ta áp dụng công thức tính diện tích sau: S= a². sin α
Ví dụ 3: Cho hình thoi ABCD, với cạnh hình thoi = 4cm, góc A = 30 độ. Tính diện tích của hình thoi ABCD.
Giải:
Theo bài ra ta có: a = 4, góc = 30 độ. Ta thay vào công thức như sau:
S = a2 x sinA = 4² x sin(30o) = 8(cm2).
Trên đây chúng tôi đã gửi đến bạn những thông tin chi tiết nhất về cách tính chu vi, diện tích của hình thoi. Nếu bạn cần hỗ trợ hay còn thắc mắc để lại thông tin bên dưới để được hỗ trợ nhé!